Difference between revisions of "The individual approach"
m |
m |
||
| Line 41: | Line 41: | ||
where | where | ||
| + | |||
::<div style="text-align: left;font-size: 12pt"><math> | ::<div style="text-align: left;font-size: 12pt"><math> | ||
| Line 48: | Line 49: | ||
If we assume that $\bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)$, then, the $y_i$'s are independent and | If we assume that $\bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)$, then, the $y_i$'s are independent and | ||
| + | |||
::<div style="text-align: left;font-size: 12pt"><math> | ::<div style="text-align: left;font-size: 12pt"><math> | ||
| Line 56: | Line 58: | ||
| − | \begin{ | + | ::<div style="text-align: left;font-size: 12pt"><math>\begin{align} |
p_Y(y_1, y_2, \ldots y_n ; \psi) &=& \prod_{j=1}^n p_{Y_j}(y_j ; \psi) \\ \\ | p_Y(y_1, y_2, \ldots y_n ; \psi) &=& \prod_{j=1}^n p_{Y_j}(y_j ; \psi) \\ \\ | ||
&& \frac{e^{-\frac{1}{2} \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi)} \right)^2}}{\prod_{j=1}^n \sqrt{2\pi g(t_j ; \psi)}} | && \frac{e^{-\frac{1}{2} \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi)} \right)^2}}{\prod_{j=1}^n \sqrt{2\pi g(t_j ; \psi)}} | ||
| Line 64: | Line 66: | ||
\begin{equation} | \begin{equation} | ||
\hat{\psi} = \argmin_{\psi} \left\{ \sum_{j=1}^n \log(g(t_j ; \psi)^2) + \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi) }\right)^2 \right \} | \hat{\psi} = \argmin_{\psi} \left\{ \sum_{j=1}^n \log(g(t_j ; \psi)^2) + \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi) }\right)^2 \right \} | ||
| − | \end{ | + | \end{align}</math></div> |
| + | |||
and the deviance is therefore | and the deviance is therefore | ||
| − | \begin{ | + | ::<div style="text-align: left;font-size: 12pt"><math>\begin{align} |
-2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) = \sum_{j=1}^n \log(g(t_j ; \hat{\psi})^2) + \sum_{j=1}^n \left(\frac{y_j - f(t_j ; \hat{\psi})}{g(t_j ; \hat{\psi})}\right)^2 +n\log(2\pi) | -2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) = \sum_{j=1}^n \log(g(t_j ; \hat{\psi})^2) + \sum_{j=1}^n \left(\frac{y_j - f(t_j ; \hat{\psi})}{g(t_j ; \hat{\psi})}\right)^2 +n\log(2\pi) | ||
| − | \end{ | + | \end{align}</math></div> |
| + | |||
| Line 77: | Line 81: | ||
For a constant error model ($y_{j} = f(t_j ; \phi) + a \, \bar{\varepsilon_j}$), we have | For a constant error model ($y_{j} = f(t_j ; \phi) + a \, \bar{\varepsilon_j}$), we have | ||
| − | \begin{ | + | |
| + | |||
| + | ::<div style="text-align: left;font-size: 12pt"><math>\begin{align} | ||
\hat{\phi} &=& \argmin_{\psi} \sum_{j=1}^n \left( y_j - f(t_j ; \phi)\right)^2 \\ \\ | \hat{\phi} &=& \argmin_{\psi} \sum_{j=1}^n \left( y_j - f(t_j ; \phi)\right)^2 \\ \\ | ||
\hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - f(t_j ; \hat{\phi})\right)^2 \\ \\ | \hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - f(t_j ; \hat{\phi})\right)^2 \\ \\ | ||
-2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) &=& \sum_{j=1}^n \log(\hat{a}^2) + n +n\log(2\pi) | -2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) &=& \sum_{j=1}^n \log(\hat{a}^2) + n +n\log(2\pi) | ||
| − | \end{ | + | \end{align}</math></div> |
A linear model has the form | A linear model has the form | ||
| − | + | ||
| + | ::<div style="text-align: left;font-size: 12pt"><math> | ||
y_{j} = F \, \phi + a \, \bar{\varepsilon_j} | y_{j} = F \, \phi + a \, \bar{\varepsilon_j} | ||
| − | + | </math></div> | |
| + | |||
The solution has then a close form | The solution has then a close form | ||
| − | \begin{ | + | |
| + | ::<div style="text-align: left;font-size: 12pt"><math>\begin{align} | ||
\hat{\phi} &=& (F^\prime F)^{-1} F^\prime y \\ | \hat{\phi} &=& (F^\prime F)^{-1} F^\prime y \\ | ||
\hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - F \hat{\phi})\right)^2 | \hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - F \hat{\phi})\right)^2 | ||
| − | \end{ | + | \end{align}</math></div> |
| + | |||
| Line 109: | Line 119: | ||
We consider the three following structural models: | We consider the three following structural models: | ||
| − | # One compartment model | + | # '''One compartment model''' |
| − | + | ||
| + | ::<div style="text-align: left;font-size: 12pt"><math> | ||
f_1(t ; V,k_e) = \frac{D}{V} e^{-k_e \, t} | f_1(t ; V,k_e) = \frac{D}{V} e^{-k_e \, t} | ||
| − | + | </math></div> | |
| + | |||
| + | |||
| + | |||
| + | # '''Two compartments model''' | ||
| − | + | ::<div style="text-align: left;font-size: 12pt"><math> | |
| − | |||
f_2(t ; V_1,V_2,k_1,k_2) = \frac{D}{V_1} e^{-k_1 \, t} + \frac{D}{V_2} e^{-k_2 \, t} | f_2(t ; V_1,V_2,k_1,k_2) = \frac{D}{V_1} e^{-k_1 \, t} + \frac{D}{V_2} e^{-k_2 \, t} | ||
| − | + | </math></div> | |
| + | |||
| + | |||
| + | |||
| + | # '''Polynomial model''' | ||
| − | + | ::<div style="text-align: left;font-size: 12pt"><math> | |
| − | |||
f_3(t ; V,\alpha,\beta,\gamma) = \frac{1}{V}(D-\alpha t - \beta t^2 - \gamma t^3) | f_3(t ; V,\alpha,\beta,\gamma) = \frac{1}{V}(D-\alpha t - \beta t^2 - \gamma t^3) | ||
| − | + | </math></div> | |
| + | |||
Revision as of 15:57, 1 February 2013
$ \DeclareMathOperator*{\argmin}{arg\,min} $
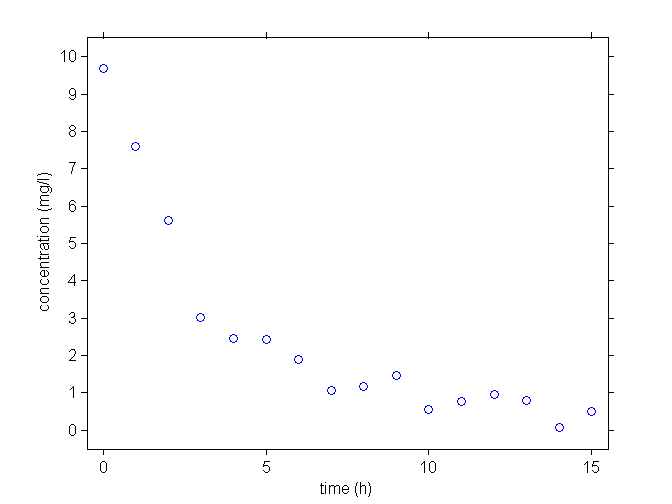
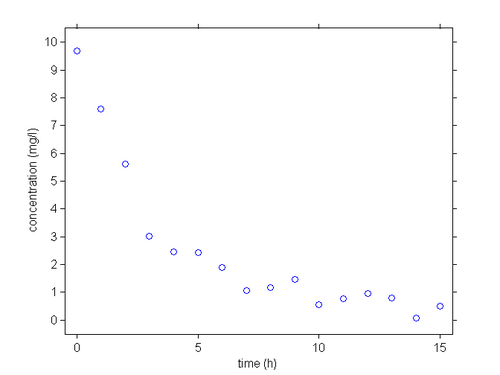
An example of continuous data from a single individual
A model for continuous data:
- \(\begin{align} y_{j} &=& f(t_j ; \psi) + \varepsilon_j \quad ; \quad 1\leq j \leq n \\ &=& f(t_j ; \psi) + g(t_j ; \psi) \bar{\varepsilon_j} \end{align}\)
- $f$ : structural model
- $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters
- $(t_1,t_2,\ldots , t_n)$ : observation times
- $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\Epsilon({\varepsilon_j}) =0$)
- $g$ : { residual error model}
- $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors $(Var(\bar{\varepsilon_j}) =1)$
Some tasks in the context of modelling, i.e. when a vector of observations $(y_j)$ is available:
- Simulate a vector of observations $(y_j)$ for a given model and a given parameter $\psi$,
- Estimate the vector of parameters $\psi$ for a given model,
- Select the structural model $f$
- Select the residual error model $g$
- Assess/validate the selected model
Maximum likelihood estimation of the parameters: $\hat{\psi}$ maximizes $L(\psi ; y_1,y_2,\ldots,y_j)$
where
- \( L(\psi ; y_1,y_2,\ldots,y_j) {\overset{def}{=}} p_Y( y_1,y_2,\ldots,y_j ; \psi) \)
If we assume that $\bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)$, then, the $y_i$'s are independent and
- \( y_{j} \sim {\cal N}(f(t_j ; \psi) , g(t_j ; \psi)^2) \)
and the p.d.f of $(y_1, y_2, \ldots y_n)$ can be computed:
- \(\begin{align} p_Y(y_1, y_2, \ldots y_n ; \psi) &=& \prod_{j=1}^n p_{Y_j}(y_j ; \psi) \\ \\ && \frac{e^{-\frac{1}{2} \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi)} \right)^2}}{\prod_{j=1}^n \sqrt{2\pi g(t_j ; \psi)}} \end{eqnarray*} Maximizing the likelihood is equivalent to minimizing the deviance (-2 '"`UNIQ-MathJax21-QINU`"' log-likelihood) which plays here the role of the objective function: \begin{equation} \hat{\psi} = \argmin_{\psi} \left\{ \sum_{j=1}^n \log(g(t_j ; \psi)^2) + \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi) }\right)^2 \right \} \end{align}\)
and the deviance is therefore
- \(\begin{align} -2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) = \sum_{j=1}^n \log(g(t_j ; \hat{\psi})^2) + \sum_{j=1}^n \left(\frac{y_j - f(t_j ; \hat{\psi})}{g(t_j ; \hat{\psi})}\right)^2 +n\log(2\pi) \end{align}\)
This minimization problem usually does not have an analytical solution for a non linear model. Some optimization procedure should be used.
For a constant error model ($y_{j} = f(t_j ; \phi) + a \, \bar{\varepsilon_j}$), we have
- \(\begin{align} \hat{\phi} &=& \argmin_{\psi} \sum_{j=1}^n \left( y_j - f(t_j ; \phi)\right)^2 \\ \\ \hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - f(t_j ; \hat{\phi})\right)^2 \\ \\ -2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) &=& \sum_{j=1}^n \log(\hat{a}^2) + n +n\log(2\pi) \end{align}\)
A linear model has the form
- \( y_{j} = F \, \phi + a \, \bar{\varepsilon_j} \)
The solution has then a close form
- \(\begin{align} \hat{\phi} &=& (F^\prime F)^{-1} F^\prime y \\ \hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - F \hat{\phi})\right)^2 \end{align}\)
A PK example
A dose of 100 mg of a drug is administrated to a patient as an intravenous (IV) bolus at time 0 and concentrations of the drug are measured every hour during 15 hours.
We consider the three following structural models:
- One compartment model
- \( f_1(t ; V,k_e) = \frac{D}{V} e^{-k_e \, t} \)
- Two compartments model
- \( f_2(t ; V_1,V_2,k_1,k_2) = \frac{D}{V_1} e^{-k_1 \, t} + \frac{D}{V_2} e^{-k_2 \, t} \)
- Polynomial model
- \( f_3(t ; V,\alpha,\beta,\gamma) = \frac{1}{V}(D-\alpha t - \beta t^2 - \gamma t^3) \)
and the four following residual error models:
| - constant error model | $g=a$, |
| - proportional error model | $g=b\, f$, |
| - combined error model | $g=a+b f$, |
Extension: $u(y_j)$ normally distributed instead of $y_j$ \begin{equation} u(y_{j}) = u(f(t_j ; \psi)) + g(t_j ; \psi)\bar{\varepsilon_j} \quad ; \quad 1\leq j \leq n \end{equation}
| - exponential error model | $\log(y)=\log(f) + a\, \bar{\varepsilon}$ |