Introduction to PK modeling using MLXPlore - Part I
Introduction
This is an introductory tutorial for describing and visualizing simple and more complex pharmacokinetic (PK) models.
We will present several PK model examples and visualize the processes of absorption, distribution and elimination that characterize them.
We will suppose in all these examples that a single dose is administered at time t=0. In each example, the modeling goal is defined. Then, the model and requests for graphical outputs are coded in MLXPlore, a new graphical and interactive software for the exploration and visualization of complex pharmacometric models. MLXPlore uses the easy and intuitive MLXtran model coding language, popularized by the Monolix software.
MLXPlore is used here for computing the predicted amount in the central compartment. We further display in the Part II the predicted amount in the depot compartment and the MLXPlore project that was used for computing it.
Absorption
First-order and zero-order absorption
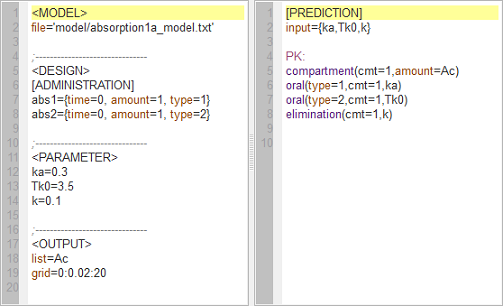
absorption1a_script: this computes and displays the amount (Ac) in the central compartment when the drug is absorbed with a first-order or zero-order absorption process.
Left: In the right-hand side window, the two (first-order and zero-order) models are described using the MLXtran coding language. In the left-hand side window, the structural model, experimental design, parameters and requested graphical output are defined.
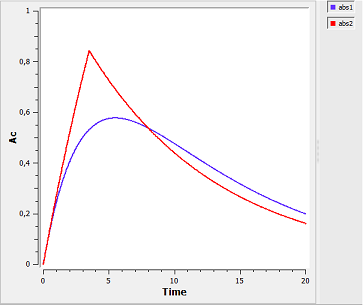
Right: The graphical output of MLXPlore, which was told to output the amount Ac in the central compartment with respect to time for zero-order (red) and first-order (blue) absorption.
See the Part II for the corresponding amounts in the depot compartment and the related $\mlxplore$ project.
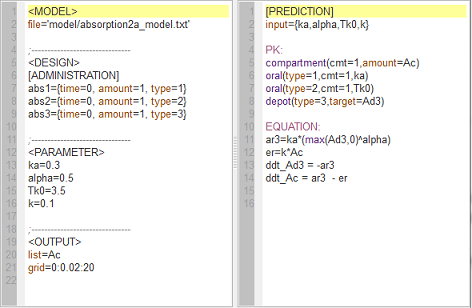
First-order, zero-order and $\alpha$-order absorption
absorption2a_script: we compute and display the amounts in the central and depot compartments when the drug is transferred from the depot to the central compartment with a first-order, zero-order or $\alpha$-order absorption process.
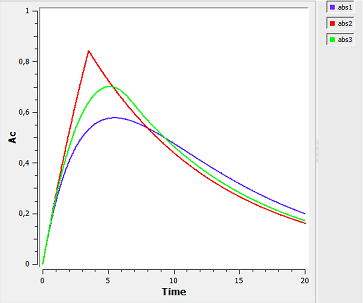
Note $\dot{A}d(t) \, = \, -ka \, \times \, Ad^{\alpha}(t).$ Zero-order absorption is obtained with $\alpha=0$ and first-order absorption with $\alpha=1$. The green curves are with respect to the $\alpha$-order absorption process.
See the Part II for the corresponding amounts in the depot compartment and the related $\mlxplore$ project.
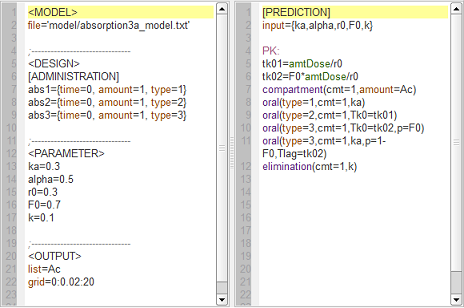
First-order, zero-order and sequential zero-order/first-order absorption
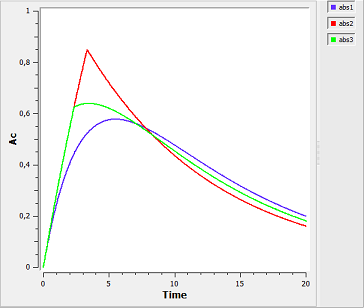
absorption3a_script: we compute and display the amount in the central compartment when the drug is transferred from the depot to the central compartment with a first-order, zero-order or sequential zero-order/first-order absorption process.
Here, $r0$ is the absorption rate for the zero-order process and $F0$ the fraction of the dose absorbed in a zero-order process. The green curves refer to the sequential zero-order/first-order absorption process.
See the Part II for the corresponding amounts in the depot compartment and the related $\mlxplore$ project.
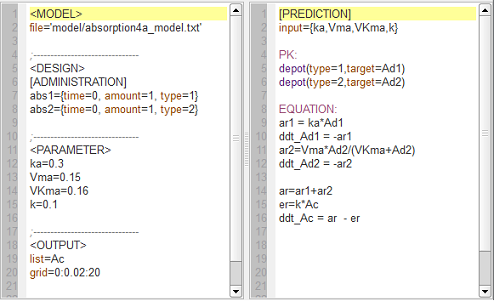
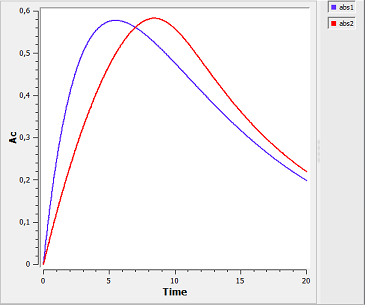
First-order and saturated absorption
absorption4_script: we compute and display the amount in the central compartment when the drug is transferred from the depot to the central compartment with a first-order or saturated (Michaelis-Mentens) absorption process. The red curve is now for the saturated absorption process.
See the Part II for the corresponding amounts in the depot compartment and the related $\mlxplore$ project.
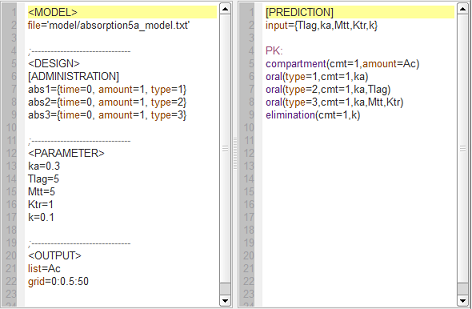
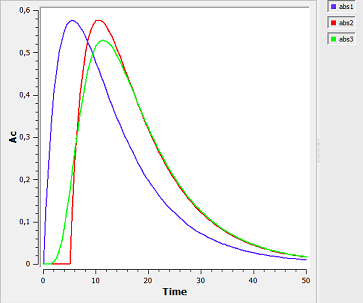
Lag-time and transit compartments
absorption5_script: we compute and display the amount in the central compartment when a lag time or a transit compartment model is used.
Here, the blue curve is for first-order absorption without lag-time, the red curve for the lag-time model and the green one for the transit compartment model. The number of transit compartments is $Ntr=Mtt/Ktr$. When $Mtt=Tlag$, the transit compartment model can be seen as a smooth version of the lag-time model. It converges to the lag-time model when the number of compartments increases (i.e., when the transfer rate constant $Ktr$ increases).
See the Part II for the corresponding amounts in the depot compartment and the related $\mlxplore$ project.
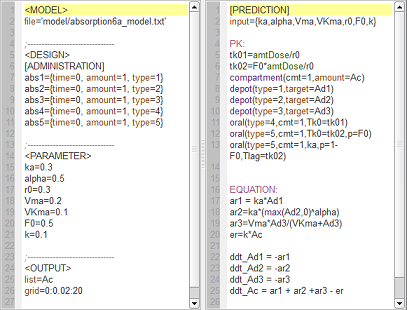
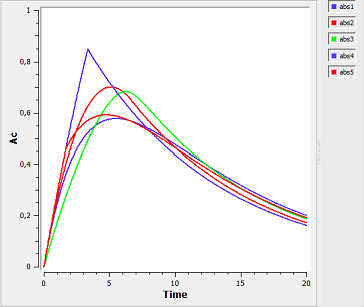
Summary
absorption6a_script: we compute and display the amount in the central compartment for all of the different absorption models presented in the previous examples.
In the figure, abs1 is first-order absorption, abs2 is $\alpha$-order absorption, abs3 is saturated absorption, abs4 is zero-order absorption and abs5 is sequential zero-order/first-order absorption.
See the Part II for the corresponding amounts in the depot compartment and the related $\mlxplore$ project.
Distribution
One, two and three compartment models
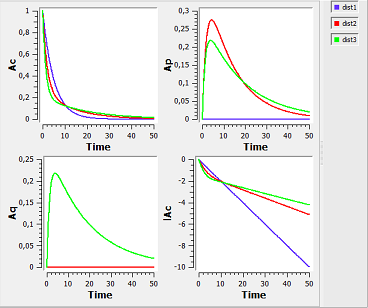
distribution1_script: we compute and display the amount in the central and peripheral compartments when the drug is distributed assuming one, two or three compartment models.
Here, $Ap$ and $Aq$ are the amounts in the first and second peripheral compartments and $lAc$ the log-amount in the central compartment.
Elimination
Linear, nonlinear and combined elimination
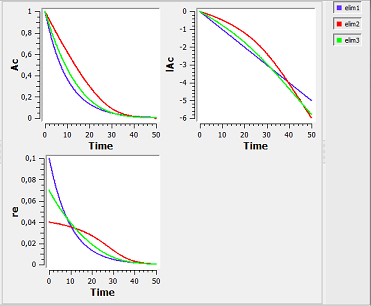
elimination1_script: we compute and display the amount in the central compartment and the rate of elimination when the drug is eliminated with a linear, nonlinear (Michaelis-Mentens) or combined elimination process (linear when $\alpha=1$ and Michaelis-Mentens when $\alpha=1$).
Here, $lAc$ is the log-amount in the central compartment and lre the log-rate of elimination of the drug. By definition, lre is a linear function of time for a linear elimination process.
All the projects shown in this session can be downloaded here: https://wiki.inria.fr/wikis/popix/images/c/c6/Pk_mlxplore.zip.