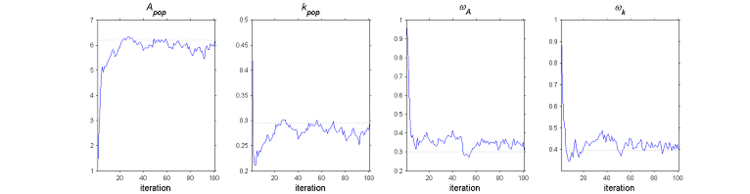
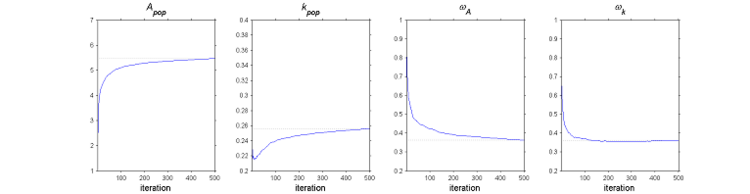
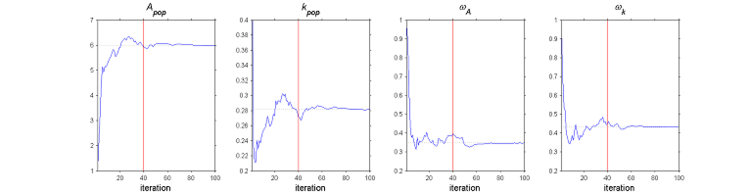
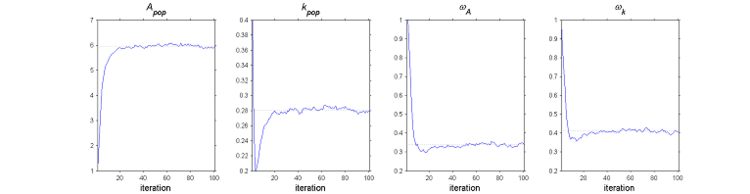
The SAEM algorithm for estimating population parameters
Contents
Introduction
The SAEM (Stochastic Approximation of EM) algorithm is a stochastic algorithm for calculating the maximum likelihood estimator (MLE) in the quite general setting of incomplete data models. SAEM has been shown to be a very powerful NLMEM tool, known to accurately estimate population parameters as well as having good theoretical properties. In fact, it converges to the MLE under very general hypotheses.
SAEM was first implemented in the $\monolix$ software. It has also been implemented in NONMEM, the R package saemix and the Matlab statistics toolbox as the function nlmefitsa.m.
Here, we consider a model that includes observations $\by=(y_i , 1\leq i \leq N)$, unobserved individual parameters $\bpsi=(\psi_i , 1\leq i \leq N)$ and a vector of parameters $\theta$. By definition, the maximum likelihood estimator of $\theta$ maximizes
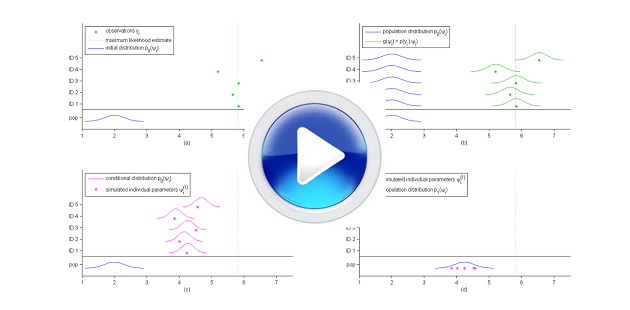
SAEM is an iterative algorithm that essentially consists of constructing $N$ Markov chains $(\psi_1^{(k)})$, ..., $(\psi_N^{(k)})$ that converge to the conditional distributions $\pmacro(\psi_1|y_1),\ldots , \pmacro(\psi_N|y_N)$, using at each step the complete data $(\by,\bpsi^{(k)})$ to calculate a new parameter vector $\theta_k$. We will present a general description of the algorithm highlighting the connection with the EM algorithm, and present by way of a simple example how to implement SAEM and use it in practice.
We will also give some extensions of the base algorithm that allow us to improve the convergence properties of the algorithm. For instance, it is possible to stabilize the algorithm's convergence by using several Markov chains per individual. Also, a simulated annealing version of SAEM allows us improve the chances of converging to the global maximum of the likelihood rather than to local maxima.
The EM algorithm
We first remark that if the individual parameters $\bpsi=(\psi_i)$ are observed, estimation is not thwarted by any particular problem because an estimator could be found by directly maximizing the joint distribution $\pypsi(\by,\bpsi ; \theta) $.
However, since the $\psi_i$ are not observed, the EM algorithm replaces $\bpsi$ by its conditional expectation. Then, given some initial value $\theta_0$, iteration $k$ updates ${\theta}_{k-1}$ to ${\theta}_{k}$ with the two following steps:
- $\textbf{E-step:}$ evaluate the quantity
- $\textbf{M-step:}$ update the estimation of $\theta$:
In can be proved that each EM iteration increases the likelihood of observations and that the EM sequence $(\theta_k)$ converges to a
stationary point of the observed likelihood under mild regularity conditions.
Unfortunately, in the framework of nonlinear mixed-effects models, there is no explicit expression for the E-step since the relationship between observations $\by$ and individual parameters $\bpsi$ is nonlinear. However, even though this expectation cannot be computed in a closed-form, it can be approximated by simulation. For instance,
- The Monte Carlo EM (MCEM) algorithm replaces the E-step by a Monte Carlo approximation based on a large number of independent simulations of the non-observed individual parameters $\bpsi$.
- The SAEM algorithm replaces the E-step by a stochastic approximation based on a single simulation of $\bpsi$.
The SAEM algorithm
At iteration $k$ of SAEM:
- $\textbf{Simulation step}$: for $i=1,2,\ldots, N$, draw $\psi_i^{(k)}$ from the conditional distribution $\pmacro(\psi_i |y_i ;\theta_{k-1})$.
- $\textbf{Stochastic approximation}$: update $Q_k(\theta)$ according to
where $(\gamma_k)$ is a decreasing sequence of positive numbers such that $\gamma_1=1$, $ \sum_{k=1}^{\infty} \gamma_k = \infty$ and $\sum_{k=1}^{\infty} \gamma_k^2 < \infty$.
- $\textbf{Maximization step}$: update $\theta_{k-1}$ according to
Implementation of SAEM is simplified when the complete model $\pmacro(\by,\bpsi;\theta)$ belongs to a regular (curved) exponential family:
where $\tilde{S}(\by,\bpsi)$ is a sufficient statistic of the complete model (i.e., whose value contains all the information needed to compute any estimate of $\theta$) which takes its values in an open subset ${\cal S}$ of $\Rset^m$. Then, there exists a function $\tilde{\theta}$ such that for any $s\in {\cal S}$,
\(
\tilde{\theta}(s) = \argmax{\theta} \left\{ - \zeta(\theta) + \langle s , \varphi(\theta) \rangle \right\} .
\)
|
(1) |
The approximation step of SAEM simplifies to a general Robbins-Monro-type scheme for approximating this conditional expectation:
- $\textbf{Stochastic approximation}$: update $s_k$ according to
Note that the E-step of EM simplifies to computing $s_k=\esp{\tilde{S}(\by,\bpsi) | \by ; \theta_{k-1}}$.
Then, both EM and SAEM algorithms use (1) for the M-step: $\theta_k = \tilde{\theta}(s_k)$.
Precise results for convergence of SAEM were obtained in the Estimation of the F.I.M. using a linearization of the model section in the case where $\pmacro(\by,\bpsi;\theta)$ belongs to a regular curved exponential family. This first version of SAEM and these first results assume that the individual parameters are simulated exactly under the conditional distribution at each iteration. Unfortunately, for most nonlinear models or non-Gaussian models, the unobserved data cannot be simulated exactly under this conditional distribution. A well-known alternative consists in using the Metropolis-Hastings algorithm: introduce a transition probability which has as unique invariant distribution the conditional distribution we want to simulate.
In other words, the procedure consists of replacing the Simulation step of SAEM at iteration $k$ by $m$ iterations of the Metropolis-Hastings (MH) algorithm described in The Metropolis-Hastings algorithm section. It was shown in the Estimation of the F.I.M. using a linearization of the model section that SAEM still converges under general conditions when coupled with a Markov chain Monte Carlo procedure.
Implementing SAEM
Implementation of SAEM can be difficult to describe when looking at complex statistical models such as mixture models, models with inter-occasion variability, etc. We are therefore going to limit ourselves to looking at some basic models in order to illustrate how SAEM can be implemented.
SAEM for a general hierarchical model
Consider first a very general model for any type (continuous, categorical, survival, etc.) of data $(y_i)$:
where $h(\psi_i)=(h_1(\psi_{i,1}), h_2(\psi_{i,2}), \ldots , h_d(\psi_{i,d}) )^\transpose$ is a $d$-vector of (transformed) individual parameters, $\mu$ a $d$-vector of fixed effects and $\Omega$ a $d\times d$ variance-covariance matrix.
We assume here that $\Omega$ is positive-definite. Then, a sufficient statistic for the complete model $\pmacro(\by,\bpsi;\theta)$ is $\tilde{S}(\bpsi) = (\tilde{S}_1(\bpsi),\tilde{S}_2(\bpsi))$, where
At iteration $k$ of SAEM, we have:
- $\textbf{Simulation step}$: for $i=1,2,\ldots, N$, draw $\psi_i^{(k)}$ from $m$ iterations of the MH algorithm described in The Metropolis-Hastings algorithm with $\pmacro(\psi_i |y_i ;\mu_{k-1},\Omega_{k-1})$ as limiting distribution.
- $\textbf{Stochastic approximation}$: update $s_k=(s_{k,1},s_{k,2})$ according to
- $\textbf{Maximization step}$: update $(\mu_{k-1},\Omega_{k-1})$ according to
What is remarkable is that it suffices to be able to calculate $\pcyipsii(y_i | \psi_i)$ for all $\psi_i$ and $y_i$ in order to be able to run SAEM. In effect, this allows the simulation step to be run using MH since the acceptance probabilities can be calculated.
SAEM for a continuous data model
Consider now a continuous data model in which the residual error variance is now constant:
Here, the individual parameters are $\psi_i=(\phi_i,a)$. The variance-covariance matrix for $\psi_i$ is not positive-definite in this case because $a$ has no variability. If we suppose that the variance matrix $\Omega$ is positive-definite, then noting $\theta=(\mu,\Omega,a)$, a natural decomposition of the model is:
The previous statistic $\tilde{S}(\bpsi) = (\tilde{S}_1(\bpsi),\tilde{S}_2(\bpsi))$ is not sufficient for estimating $a$. Indeed, we need an additional component which is a function both of $\by$ and $\bpsi$:
Then,
The choice of step-size $(\gamma_k)$ is extremely important for ensuring convergence of SAEM. The sequence $(\gamma_k)$ used in \monolix decreases like $k^{-\alpha}$. We recommend using $\alpha=0$ (that is, $\gamma_k=1$) during the first $K_1$ iterations, in order to converge quickly to a neighborhood of a maximum of the likelihood, and $\alpha=1$ during the next $K_2$ iterations. Indeed, the initial guess $\theta_0$ may be far from the maximum likelihood value we are looking for, and the first iterations with $\gamma_k=1$ allow SAEM to converge quickly to a neighborhood of this value. Following this, smaller step-sizes ensure the almost sure convergence of the algorithm to the maximum likelihood estimator.
A simple example to understand why SAEM converges in practice
Let us look at a very simple Gaussian model, with only one observation per individual:
We will furthermore assume that both $\omega^2$ and $\sigma^2$ are known.
Here, the maximum likelihood estimator $ \hat{\theta}$ of $\theta$ is easy to compute since $y_i \sim_{i.i.d.} {\cal N}(\theta,\omega^2+\sigma^2)$. We find that
We now propose to try and compute $\hat{\theta}$ using SAEM instead. The simulation step is straightforward since the conditional distribution of $\psi_i$ is a normal distribution:
where
The maximization step is also straightforward. Indeed, a sufficient statistics for estimating $\theta$ is
Then,
Let us first look at the behavior of SAEM when $\gamma_k=1$. At iteration $k$,
- Simulation step: $\psi_i^{(k)} \sim {\cal N}( a \theta_{k-1} + (1-a)y_i , \gamma^2). $
- Maximization step: $\theta_k = \displaystyle{ \frac{ {\cal S}(\bpsi^{(k)})}{N} } = \displaystyle{ \frac{1}{N} }\sum_{i=1}^{N} \psi_i^{(k)}$.
It can be shown that:
where $e_k \sim {\cal N}(0, \gamma^2 /N)$. Then, the sequence $(\theta_k)$ is an autoregressive process of order 1 (AR(1)) which converges in distribution to a normal distribution when $k\to \infty$:
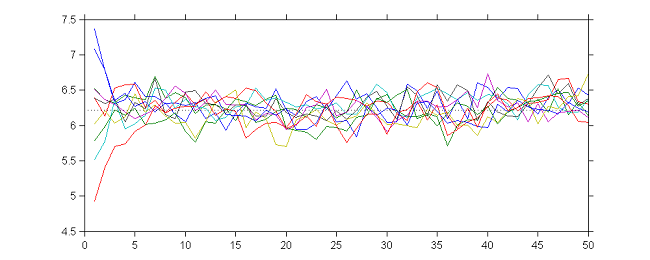 |
10 sequences $(\theta_k)$ obtained with different initial values and $\gamma_k=1$ for $1\leq k \leq 50$
|
Now, let us see what happens instead when $\gamma_k$ decreases like $1/k$. At iteration $k$,
- Simulation step: $\psi_i^{(k)} \sim {\cal N}( a \theta_{k-1} + (1-a)y_i , \gamma^2) $
- Maximization step:
- Here, we can show that:
- where $e_k \sim {\cal N}(0, \gamma^2 /N)$. Then, the sequence $(\theta_k)$ converges almost surely to $\hat{\theta}$.
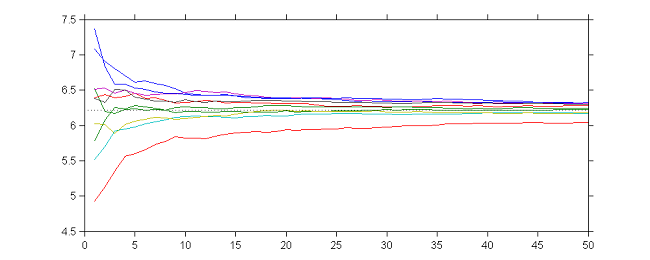 |
10 sequences $(\theta_k)$ obtained with different initial values and $\gamma_k=1/k$ for $1\leq k \leq 50$
|
Thus, we see that by combining the two strategies, the sequence $(\theta_k)$ is a Markov chain that converges to a random walk around $\hat{\theta}$ during the first $K_1$ iterations, then converges almost surely to $\hat{\theta}$ during the next $K_2$ iterations.
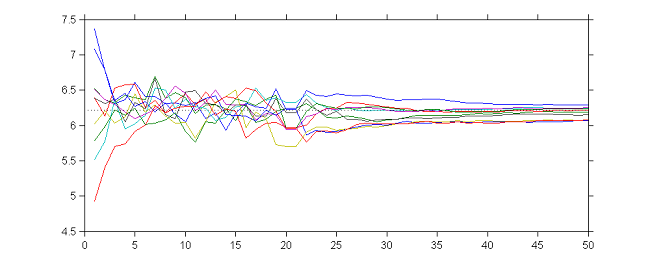 |
10 sequences $(\theta_k)$ obtained with different initial values, $\gamma_k=1$ for $1\leq k \leq 20$ and $\gamma_k=1/(k-20)$ for $21\leq k \leq 50$
|
The SAEM algorithm in practice.
|
A simulated annealing version of SAEM
Convergence of SAEM can strongly depend on the initial guess when the likelihood ${\like}$ has several local maxima. A simulated annealing version of SAEM can improve convergence of the algorithm toward the global maximum of ${\like}$.
To detail this, we can first rewrite the joint pdf of $(\by,\bpsi)$ as follows:
where $C(\theta)$ is a normalizing constant that only depends on $\theta$.
Then, for any "temperature" $T\geq0$, we consider the complete model
where $C_T(\theta)$ is still a normalizing constant.
We then introduce a decreasing temperature sequence $(T_k, 1\leq k \leq K)$ and use the SAEM algorithm on the complete model $\pmacro_{T_k}(\by,\bpsi;\theta)$ at iteration $k$ (the usual version of SAEM uses $T_k=1$ at each iteration). The sequence $(T_k)$ is chosen to have large positive values during the first iterations, then decrease with an exponential rate to 1: $ T_k = \max(1, \tau \ T_{k-1}) $.
Consider for example the following model for continuous data:
Here, $\theta = (\mu,\Omega,a^2)$ and
where $C(\theta)$ is a normalizing constant that only depends on $a$ and $\Omega$.
We see that $\pmacro_T(\by,\bpsi;\theta)$ will also be a normal distribution whose residual error variance $a^2$ is replaced by $T a^2$ and variance matrix $\Omega$ for the random effects by $T\Omega$.
In other words, a model with a "large temperature" is a model with large variances.
The algorithm therefore consists in choosing large initial variances $\Omega_0$ and $a^2_0$ (that include the initial temperature $T_0$ implicitly) and setting $ a^2_k = \max(\tau \ a^2_{k-1} , \hat{a}(\by,\bpsi^{(k)}) $ and $ \Omega_k = \max(\tau \ \Omega_{k-1} , \hat{\Omega}(\bpsi^{(k)}) $ during the first iterations. Here, $0\leq\tau\leq 1$.
These large values of the variance make the conditional distributions $\pmacro_T(\psi_i | y_i;\theta)$ less concentrated around their modes, and thus allows the sequence $(\theta_k)$ to "escape" from local maxima of the likelihood during the first iterations of SAEM and converge to a neighborhood of the global maximum of ${\like}$. After these initial iterations, the usual SAEM algorithm is used to estimate these variances at each iteration.