Estimation of the log-likelihood

The observed log-likelihood ${\llike}(\theta;\by)=\log({\like}(\theta;\by))$ can be estimated without any approximation of the model using a Monte-Carlo approach.

Since

$ \begin{eqnarray} {\llike}(\theta;\by) &\eqdef& \log(\py(\by;\theta)) \\ &=& \sum_{i=1}^{N} \log(\pyi(y_i;\theta)), \end{eqnarray}$

we will estimate the log-pdf $\log(\pyi(y_i;\theta))$ for each individual and derive an estimate of the log-likelihood as the sum of these individual log-likelihoods. We will explain here how to estimate the log-pdf $\log(\pyi(y_i;\theta))$ for any individual $i$.

Using the $\phi$-representation of the model, notice first that $\pyi(y_i;\theta)$ can be decomposed as follows

$\begin{eqnarray} \pyi(y_i;\theta) &=& \displaystyle{ \int \pyipsii(y_i,\phi_i;\theta)\,d\phi_i }\\ &=& \displaystyle{ \int \pcyiphii(y_i | \phi_i;\theta)\pphii(\phi_i;\theta)\,d\phi_i }\\ &=& \esps{\qphii}{\pcyiphii(y_i | \phi_i;\theta)}. \end{eqnarray}$

$\pyi(y_i;\theta)$ is expressed as a mean. It can therefore be approximated by an empirical mean using a Monte-Carlo procedure:

1. draw $M$ independent realizations $\phi_i^{(1)}$, $\phi_i^{(2)}$, ..., $\phi_i^{(M)}$ of the normal distribution $\qphii(\, \cdot \, ; \theta)$,

2. estimate $ \pyi(y_i;\theta)$ with

$ \hat{p}_{i,M} = \displaystyle{ \frac{1}{M} } \sum_{m=1}^{M}\pcyiphii(y_i | \phi_i^{(m)};\theta) $

By construction, this estimator is unbiased:

$\begin{eqnarray} \esp{\hat{p}_{i,M} }&=& \esps{\qphii}{\pcyiphii(y_i | \phi_i^{(m)};\theta)} \\ &=& \pyi(y_i;\theta) \end{eqnarray}$

Furthermore, it is consistent since its variance decreases as $1/M$:

$ \var{\hat{p}_{i,M} }= \displaystyle{\frac{1}{M} }\vars{\qphii}{\pcyiphii(y_i | \phi_i^{(m)};\theta)}. $

We could be satisfied with this estimator, since we "only" have to select $M$ large enough to get an estimator with a small variance. Nevertheless, we will see now that it is possible to improve the statistical properties of this estimator.

For any distribution $\tqphii$ absolutely continuous with respect to the marginal distribution $\qphii$, we can write

$\begin{eqnarray} \displaystyle{ \int \pyiphii(y_i,\phi_i;\theta)\,d\phi_i }\\ &=& \displaystyle{ \int \pcyiphii(y_i | \phi_i;\theta)\frac{\pphii(\phi_i;\theta)}{\tpphii(\phi_i;\theta)}\tpphii(\phi_i;\theta)\,d\phi_i }\\ &=& \esps{\tqphii}{\pcyiphii(y_i | \phi_i;\theta)\displaystyle{\frac{\pphii(\phi_i;\theta)}{\tpphii(\phi_i;\theta)} } }. \end{eqnarray}$

We can now approximate $\pyi(y_i;\theta)$ via an Importance Sampling integration method using $\tqphii$ as a proposal distribution:

1. draw $M$ independent realizations $\phi_i^{(1)}$, $\phi_i^{(2)}$, ..., $\phi_i^{(M)}$ of the proposal distribution $\tqphii(\, \cdot \, ; \theta)$,
2. estimate $ \pyi(y_i;\theta)$ with

$ \hat{p}_{i,M} = \displaystyle{ \frac{1}{M} }\sum_{m=1}^{M}\pcyiphii(y_i | \phi_i^{(m)};\theta) \displaystyle{\frac{\pphii(\phi_i^{(m)};\theta)}{\tpphii(\phi_i^{(m)};\theta)} } $

By construction, this new estimator is also unbiased and its variance decreases also as $1/M$:

$ \var{\hat{p}_{i,M} }= \displaystyle{\frac{1}{M} }\vars{\tqphii}{\pcyiphii(y_i | \phi_i^{(m)};\theta)\displaystyle{ \frac{\pphii(\phi_i^{(m)};\theta)}{\tpphii(\phi_i^{(m)};\theta)} } }. $

There exists an infinite number of possible proposal distributions $\tpphii$ which all provide the same rate of convergence $1/M$. The trick is to reduce the variance of the estimator by selecting a proposal such that the numerator is as small as possible.

Imagine that we use the conditional distribution $\qcphiiyi$ as proposal. Then, for any $m=1,2,\ldots,M$,

$\begin{eqnarray} \pcyiphii(y_i | \phi_i^{(m)};\theta) \displaystyle{ \frac{\pphii(\phi_i^{(m)};\theta)}{\tpphii(\phi_i^{(m)};\theta)} } &=& \pcyiphii(y_i | \phi_i^{(m)};\theta) \displaystyle{ \frac{\pphii(\phi_i^{(m)};\theta)}{\pcphiiyi(\phi_i^{(m)} | y_i;\theta)} } \\ &=& \pyi(y_i;\theta) \end{eqnarray}$

which means that $\hat{p}_{i,M}=\pyi(y_i;\theta)$! Such an estimator is optimal since its variance is null and only one realization of $\qcphiiyi$ suffices for computing exactly $\pyi(y_i;\theta)$. The problem is that it is not possible to generate the $\phi_i^{(m)}$'s with this conditional distribution, since that would require to compute a normalizing constant ... which is precisely $\pyi(y_i;\theta)$.

Nevertheless, this conditional distribution can be estimated using the Metropolis-Hastings algorithm described in The Metropolis-Hastings algorithm section and a practical proposal "close" to the optimal proposal $\qcphiiyi$ can be derived. We can then expect to get a very accurate estimation with a relatively small Monte-Carlo size $M$.

In $\monolix$, the mean and variance of the conditional distribution $\qcphiiyi$ are estimated by M-H for each individual $i$. Then, the $\phi_i^{(m)}$'s are drawn with a non-central $t$ distribution:

$\phi_i^{(m)} = \mu_i + \sigma_i \times T_{i,m} $

where $\mu_i$ and $\sigma^2_i$ are estimates of $\esp{\phi_i|y_i;\theta}$ and $\var{\phi_i|y_i;\theta}$, and where $(T_{i,m})$ is a sequence of i.i.d. random variables distributed with a Student'$t-$distribution with $\nu$ degrees of freedom.

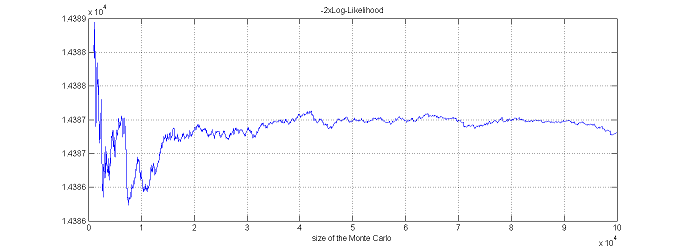
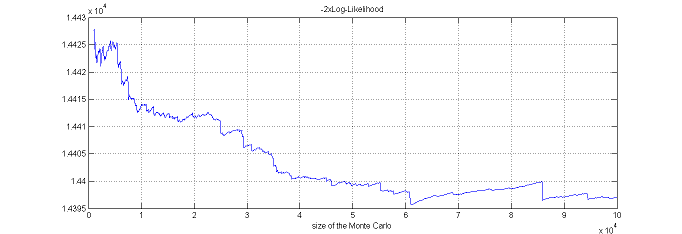
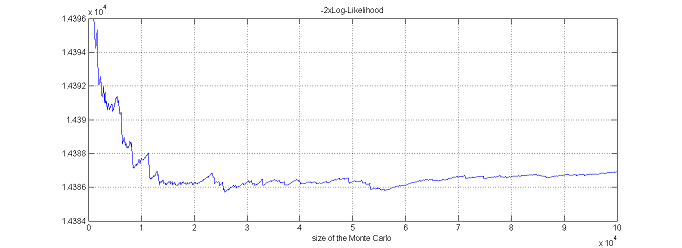
$\monolix$ uses the default value $\nu=5$. It is possible to use the default value $\nu=5$. It is also possible to automatically test different d.f in $\{2, 5, 10, 20\}$ and to select the one that provides the smallest empirical variance for $\widehat{ {\llike} }_M(\theta;\by) = \sum_{i=1}^{N}\log(\hat{p}_{i,M})$.

Remark

Even if $\widehat{\like}_M(\theta;\by) = \prod_{i=1}^{N}\hat{p}_{i,M}$ is an unbiased estimator of ${\like}(\theta;\by)$,

$\widehat{ {\llike} }_M(\theta;\by)$ is a biased estimator of $\log({\like}(\theta;\by))$. Indeed, by Jensen's inequality, we have that

$ \esp{\log(\widehat{ {\like} }_M(\theta;\by))} \leq \log \esp{\widehat{ {\like} }_M(\theta;\by)} = \log ({\like}(\theta;\by)). $

But, i) the bias decreases as $M$ increases, ii) the bias is reduced if $\widehat{ {\like} }_M(\theta;\by)$ is close to ${\like}(\theta;\by)$. It is therefore highly recommended to use a proposal as close as possible to the conditional distribution $\qcphiiyi$, which means to estimate this conditional distribution before estimating the log-likelihood.

Example

A mixture model is used for this example. We don't aim here to provide the details about the model and the formulas used for implementing the algorithm. We use this example to highlight the importance of the choice of the proposal distribution for estimating the likelihood in complex models.

The three graphics below display the estimation of the deviance ($-2\times {\llike}(\theta;\by)$) by Importance Sampling using different proposal distributions. The estimated deviance is displayed as a function of the Monte-Carlo size.

In this first example, the conditional distributions of the individual parameters $\phi_i$ were estimated using the M-H algorithm and non-central $t$ distributions with 5 $d.f.$ we used as proposal distributions. There is no bias and an accurate estimation is obtained with a small Monte-Carlo size. The estimated deviance is 14386.8 (s.e. = 0.7). Here, only 100 iterations of the M-H were enough for correctly estimating the conditional means and variances of the $\psi_i$.

In this second example, only the last 30 iterations of SAEM were used for estimating the conditional mean and variances of the $\phi_i$. Then, non-central $t$ distributions with 5 $d.f.$ we used as proposal distributions. There is a bias which decreases very slowly with the Monte-Carlo size and which is not negligible even with $10^5$ simulations: the estimated deviance is 14397.0 (s.e. = 2.7).

Normal distributions were used in this example as proposals. The parameters of these distributions were the means and variances of the conditional distributions of the $\phi_i$ estimated using the M-H algorithm. Results are similar to those obtained with a $t$ distribution(estimated deviance=14386.9, s.e. = 1) but more simulations are required for eliminating the bias.

Estimation of the log-likelihood via linearization

For continuous data models, an alternative to the Importance Sampling approach is to use a linearization of the model, following what was proposed in Estimation of the F.I.M. using a linearization of the model section for approximating the observed Fisher Information Matrix. Indeed, the marginal distribution of a continuous vector of observations $y_i$ can be approximated by a normal distribution. It is then straightforward to derive the associated likelihood. All the calculations are detailed in ???? Section.

This method can be much faster than Importance Sampling. It should be used by the modeler for model selection purpose during the first runs, when the goal is to identify significant differences between models. Importance Sampling should be used when a more precise evaluation of the log-likelihood is required.

Estimation of the log-likelihood

Estimation of the log-likelihood via linearization

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

WikiPopix

Introduction

Models

Tasks & Tools

Methods

Download files

Tools