Difference between revisions of "Overview"
Jump to navigation
Jump to search
m |
m |
||
| Line 9: | Line 9: | ||
The classical [[Media:individualModel.pdf|''individual approach'']] derives a model for a unique individual. | The classical [[Media:individualModel.pdf|''individual approach'']] derives a model for a unique individual. | ||
| + | |||
| + | |||
| + | :: <math>x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0</math> | ||
* Predicted concentration at time $t$: | * Predicted concentration at time $t$: | ||
\begin{equation} | \begin{equation} | ||
| − | |||
f(t ; V,k) = \frac{D}{V} \ e^{-k \, t} | f(t ; V,k) = \frac{D}{V} \ e^{-k \, t} | ||
\end{equation} | \end{equation} | ||
Revision as of 15:13, 1 February 2013
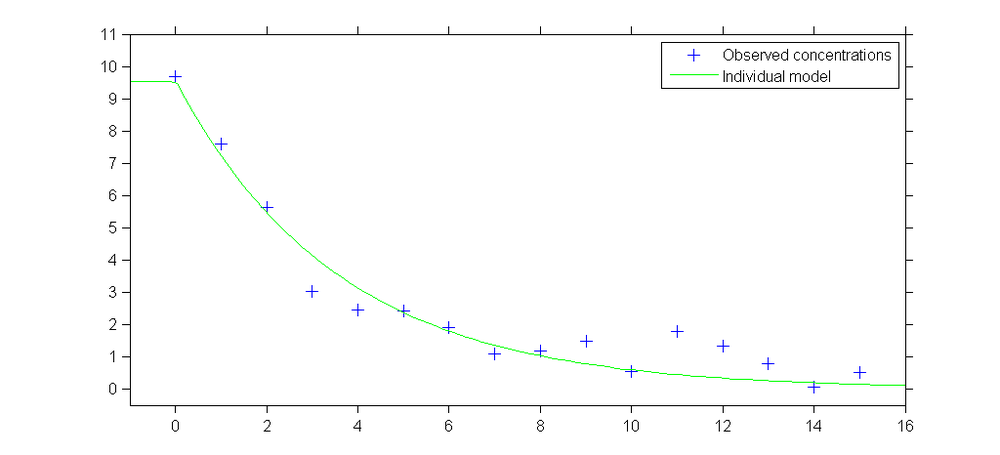
Data: concentrations at times $0, 1, \ldots 15$, from 6 patients who received each 100 mg at time $t=0$ (bolus intravenous):
Goal of modelling: describe the variability of the data (structural, intra $\&$ inter variabilities) using a statistical model.
The classical individual approach derives a model for a unique individual.
- \[x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]
- Predicted concentration at time $t$:
\begin{equation} f(t ; V,k) = \frac{D}{V} \ e^{-k \, t} \end{equation}
- Observed concentration at time $t_j$, $j=1, 2, \ldots, 15$:
\begin{equation} y_j = f(t_j ; V,k) + \varepsilon_j \end{equation}
Observed concentrations from individual 1 and predicted concentration profile obtained with $V=10.5$ and $k=0.279$: