Difference between revisions of "The individual approach"
m |
m |
||
| Line 1: | Line 1: | ||
| + | \usepackage{amsmath} | ||
| + | \newcommand{\argmin}{\operatornamewithlimits{argmin}} | ||
| + | |||
An example of continuous data from a single individual | An example of continuous data from a single individual | ||
| Line 12: | Line 15: | ||
| − | * $f$ : | + | * $f$ : structural model |
* $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters | * $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters | ||
* $(t_1,t_2,\ldots , t_n)$ : observation times | * $(t_1,t_2,\ldots , t_n)$ : observation times | ||
* $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\Epsilon({\varepsilon_j}) =0$) | * $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\Epsilon({\varepsilon_j}) =0$) | ||
* $g$ : { residual error model} | * $g$ : { residual error model} | ||
| − | * $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors ( | + | * $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors (Var({\bar{\varepsilon_j}}) =1) |
Some tasks in the context of modelling, {\i.e.} when a vector of observations $(y_j)$ is available: | Some tasks in the context of modelling, {\i.e.} when a vector of observations $(y_j)$ is available: | ||
| + | |||
* Simulate a vector of observations $(y_j)$ for a given model and a given parameter $\psi$, | * Simulate a vector of observations $(y_j)$ for a given model and a given parameter $\psi$, | ||
| Line 29: | Line 33: | ||
| − | Maximum likelihood estimation of the parameters: | + | Maximum likelihood estimation of the parameters: $\hat{\psi}$ maximizes $L(\psi ; y_1,y_2,\ldots,y_j) |
| − | |||
| − | $\hat{\psi}$ maximizes $L(\psi ; y_1,y_2,\ldots,y_j) | ||
| − | |||
where | where | ||
| Line 39: | Line 40: | ||
\end{equation} | \end{equation} | ||
| − | If we assume that $ \bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)$, then, the $y_i$'s are independent and | + | |
| + | If we assume that $\bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)$, then, the $y_i$'s are independent and | ||
| + | |||
\begin{equation} | \begin{equation} | ||
y_{j} \sim {\cal N}(f(t_j ; \psi) , g(t_j ; \psi)^2) | y_{j} \sim {\cal N}(f(t_j ; \psi) , g(t_j ; \psi)^2) | ||
| Line 45: | Line 48: | ||
and the p.d.f of $(y_1, y_2, \ldots y_n)$ can be computed: | and the p.d.f of $(y_1, y_2, \ldots y_n)$ can be computed: | ||
| + | |||
\begin{eqnarray*} | \begin{eqnarray*} | ||
| − | p_Y(y_1, y_2, \ldots y_n ; \psi) &=& \prod_{j=1}^n p_{Y_j}(y_j ; \psi) \\ | + | p_Y(y_1, y_2, \ldots y_n ; \psi) &=& \prod_{j=1}^n p_{Y_j}(y_j ; \psi) \\ \\ |
&& \frac{e^{-\frac{1}{2} \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi)} \right)^2}}{\prod_{j=1}^n \sqrt{2\pi g(t_j ; \psi)}} | && \frac{e^{-\frac{1}{2} \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi)} \right)^2}}{\prod_{j=1}^n \sqrt{2\pi g(t_j ; \psi)}} | ||
\end{eqnarray*} | \end{eqnarray*} | ||
| Line 53: | Line 57: | ||
Maximizing the likelihood is equivalent to minimizing the deviance (-2 $\times$ log-likelihood) which plays here the role of the objective function: | Maximizing the likelihood is equivalent to minimizing the deviance (-2 $\times$ log-likelihood) which plays here the role of the objective function: | ||
\begin{equation} | \begin{equation} | ||
| − | \hat{\psi} = | + | \hat{\psi} = Argmin{\psi} \left\{ \sum_{j=1}^n \log(g(t_j ; \psi)^2) + \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi) }\right)^2 \right \} |
\end{equation} | \end{equation} | ||
Revision as of 12:44, 29 January 2013
\usepackage{amsmath} \newcommand{\argmin}{\operatornamewithlimits{argmin}}
An example of continuous data from a single individual
A model for continuous data:
\begin{eqnarray*}
y_{j} &=& f(t_j ; \psi) + \varepsilon_j \quad ; \quad 1\leq j \leq n \\ \\
&=& f(t_j ; \psi) + g(t_j ; \psi) \bar{\varepsilon_j}
\end{eqnarray*}
- $f$ : structural model
- $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters
- $(t_1,t_2,\ldots , t_n)$ : observation times
- $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\Epsilon({\varepsilon_j}) =0$)
- $g$ : { residual error model}
- $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors (Var({\bar{\varepsilon_j}}) =1)
Some tasks in the context of modelling, {\i.e.} when a vector of observations $(y_j)$ is available:
- Simulate a vector of observations $(y_j)$ for a given model and a given parameter $\psi$,
- Estimate the vector of parameters $\psi$ for a given model,
- Select the structural model $f$
- Select the residual error model $g$
- Assess/validate the selected model
Maximum likelihood estimation of the parameters: $\hat{\psi}$ maximizes $L(\psi ; y_1,y_2,\ldots,y_j)
where
\begin{equation}
L(\psi ; y_1,y_2,\ldots,y_j) {\overset{def}{=}} p_Y( y_1,y_2,\ldots,y_j ; \psi)
\end{equation}
If we assume that $\bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)$, then, the $y_i$'s are independent and
\begin{equation}
y_{j} \sim {\cal N}(f(t_j ; \psi) , g(t_j ; \psi)^2)
\end{equation}
and the p.d.f of $(y_1, y_2, \ldots y_n)$ can be computed:
\begin{eqnarray*}
p_Y(y_1, y_2, \ldots y_n ; \psi) &=& \prod_{j=1}^n p_{Y_j}(y_j ; \psi) \\ \\
&& \frac{e^{-\frac{1}{2} \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi)} \right)^2}}{\prod_{j=1}^n \sqrt{2\pi g(t_j ; \psi)}}
\end{eqnarray*}
Maximizing the likelihood is equivalent to minimizing the deviance (-2 $\times$ log-likelihood) which plays here the role of the objective function:
\begin{equation}
\hat{\psi} = Argmin{\psi} \left\{ \sum_{j=1}^n \log(g(t_j ; \psi)^2) + \sum_{j=1}^n \left( \frac{y_j - f(t_j ; \psi)}{g(t_j ; \psi) }\right)^2 \right \}
\end{equation}
and the deviance is therefore
\begin{eqnarray*}
-2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) = \sum_{j=1}^n \log(g(t_j ; \hat{\psi})^2) + \sum_{j=1}^n \left(\frac{y_j - f(t_j ; \hat{\psi})}{g(t_j ; \hat{\psi})}\right)^2 +n\log(2\pi)
\end{eqnarray*}
This minimization problem usually does not have an analytical solution for a non linear model. Some optimization procedure should be used.
For a constant error model ($y_{j} = f(t_j ; \phi) + a \, \teps_j$), we have
\begin{eqnarray*}
\hat{\phi} &=& \argmin{\psi} \sum_{j=1}^n \left( y_j - f(t_j ; \phi)\right)^2 \\
\hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - f(t_j ; \hat{\phi})\right)^2 \\
-2 LL(\hat{\psi} ; y_1,y_2,\ldots,y_j) &=& \sum_{j=1}^n \log(\hat{a}^2) + n +n\log(2\pi)
\end{eqnarray*}
A linear model has the form
\begin{equation}
y_{j} = F \, \phi + a \, \teps_j
\end{equation}
The solution has then a close form
\begin{eqnarray*}
\hat{\phi} &=& (F^\prime F)^{-1} F^\prime y \\
\hat{a}&=& \frac{1}{n}\sum_{j=1}^n \left( y_j - F \hat{\phi})\right)^2
\end{eqnarray*}
=='"`UNIQ--h-0--QINU`"''''A PK example'''==
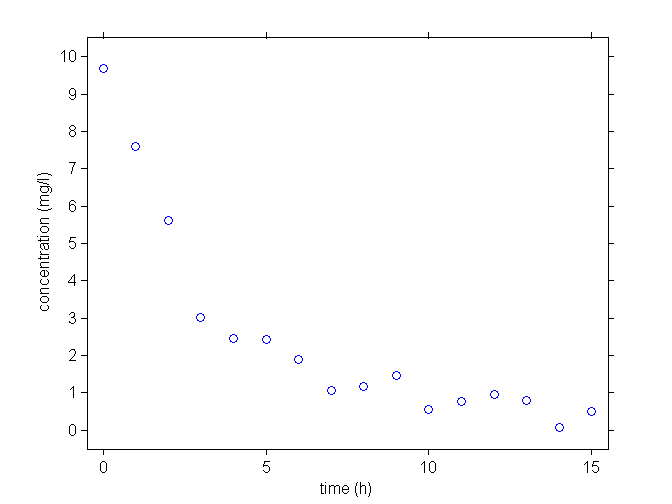
A dose of 100 mg of a drug is administrated to a patient as an intravenous (IV) bolus at time 0 and concentrations of the drug are measured every hour during 15 hours.
[[Image:graf1.png|center|800px]]
We consider the three following structural models:
# One compartment model
\begin{equation}
f_1(t ; V,k_e) = \frac{D}{V} e^{-k_e \, t} '"`UNIQ-MathJax1-QINU`"'
\end{equation}
# Polynomial model
'"`UNIQ-MathJax2-QINU`"'
and the four following residual error models:
{|
aaapower proportional error model \= $g=a+b*f$, \= \kill \\
- constant error model \> $g=a$, \\
- proportional error model \> $g=b\, f$,\\
- combined error model \> $g=a+b f$, \\
\end{tabbing}
\underline{Extension}: $u(y_j)$ normally distributed instead of $y_j$
'"`UNIQ-MathJax3-QINU`"'
\begin{tabbing}
aaapower proportional error model \= $g=a+b*f$, \= \kill \\
- exponential error model \> $\log(y)=\log(f) + a\, \teps$
\end{tabbing}