Difference between revisions of "Overview"
Jump to navigation
Jump to search
m |
m |
||
| Line 2: | Line 2: | ||
Data: concentrations at times $0, 1, \ldots 15$, from 6 patients who received each 100 mg at time $t=0$ (bolus intravenous): | Data: concentrations at times $0, 1, \ldots 15$, from 6 patients who received each 100 mg at time $t=0$ (bolus intravenous): | ||
| − | :[[Image:Intro1.png| | + | :[[Image:Intro1.png|left|900px]] |
| − | |||
| + | <br><br><br><br><br><br><br> | ||
Goal of modelling: describe the variability of the data (structural, intra $\&$ inter variabilities) using a ''statistical model''. | Goal of modelling: describe the variability of the data (structural, intra $\&$ inter variabilities) using a ''statistical model''. | ||
Revision as of 14:29, 4 February 2013
Data: concentrations at times $0, 1, \ldots 15$, from 6 patients who received each 100 mg at time $t=0$ (bolus intravenous):
Goal of modelling: describe the variability of the data (structural, intra $\&$ inter variabilities) using a statistical model.
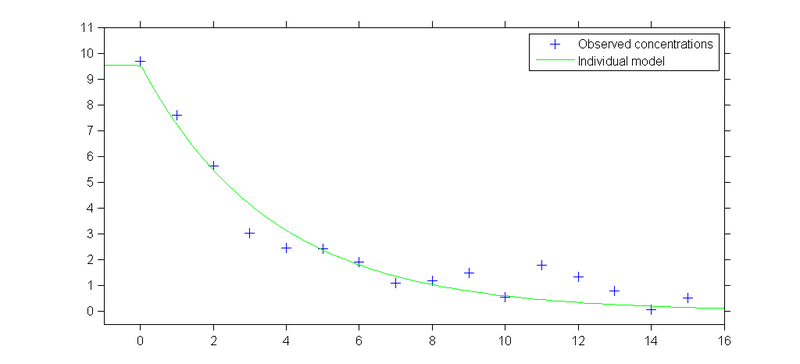
The classical individual approach derives a model for a unique individual.
- Predicted concentration at time $t$:
- \( f(t ; V,k) = \frac{D}{V} \ e^{-k \, t} \)
- Observed concentration at time $t_j$, $j=1, 2, \ldots, 15$:
- \( y_j = f(t_j ; V,k) + \varepsilon_j \)
Observed concentrations from individual 1 and predicted concentration profile obtained with $V=10.5$ and $k=0.279$: