Difference between revisions of "Animations & Videos"
Jump to navigation
Jump to search
m (→Introduction to the population approach) |
m (→Introduction to PK modeling) |
||
| (16 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
== Introduction to the population approach == | == Introduction to the population approach == | ||
| − | The | + | The goal of this animation is to show that the population approach is relevant to many fields of application (biology, agronomy, toxicology, pharmacology, etc.) and to present a PK modeling application in a bit more detail. |
| − | {{ | + | {{ShowVideo_NoCaption|image=IntroductionPA.png|size=500px|video=http://team.inria.fr/popix/files/2012/01/Populations.swf}} |
| Line 13: | Line 13: | ||
This animation describes how complex biological phenomena can be approximated by simplified models represented by mathematical equations. | This animation describes how complex biological phenomena can be approximated by simplified models represented by mathematical equations. | ||
| + | {{ShowVideo_NoCaption|image=IntroductionPK.png |size=500px|video=https://team.inria.fr/popix/files/2013/02/PKmodelling.swf }} | ||
| − | |||
| − | + | Examples of PK modeling using $\mlxplore$ can be visualized [[Introduction_to_PK_modeling_using_MLXPlore_-_Part_I|here]]. | |
| − | <br> | + | <br><br> |
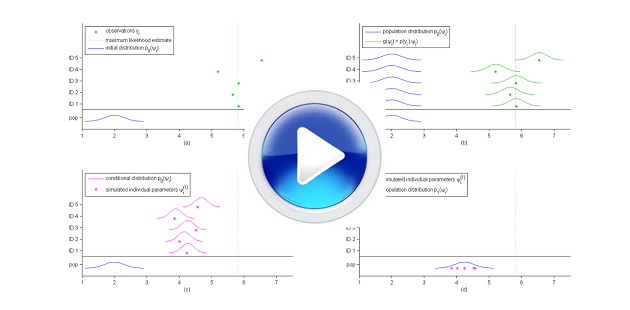
== The SAEM algorithm in practice == | == The SAEM algorithm in practice == | ||
| + | This video shows how the SAEM algorithm works, as described in [[The SAEM algorithm for estimating population parameters]] section. | ||
| − | {{ | + | {{ShowVideo_NoCaption|image=saem5b.png|video=http://popix.lixoft.net/images/2/20/saem.mp4}} |
Latest revision as of 13:44, 5 June 2013
Introduction to the population approach
The goal of this animation is to show that the population approach is relevant to many fields of application (biology, agronomy, toxicology, pharmacology, etc.) and to present a PK modeling application in a bit more detail.
Introduction to PK modeling
This animation describes how complex biological phenomena can be approximated by simplified models represented by mathematical equations.
Examples of PK modeling using $\mlxplore$ can be visualized here.
The SAEM algorithm in practice
This video shows how the SAEM algorithm works, as described in The SAEM algorithm for estimating population parameters section.