Difference between revisions of "Overview"
m |
m |
||
| Line 1: | Line 1: | ||
| + | La modélisation d'un phénomène biologique ou physique est généralement motivée par l'observation de ce phénomène, c'est à dire lorsque des données générées par ce phénomène peuvent être recueillies. Quoi de plus naturel par conséquent, que de commencer par regarder quelques données ? | ||
| + | |||
| + | {{ExampleWithImage | ||
| + | |text= This first graphics display the viral load of four patients with hepatitis C who start a treatment at time $t=0$. | ||
| + | |image = intro1.png | ||
| + | }} | ||
| − | + | {{ExampleWithImage | |
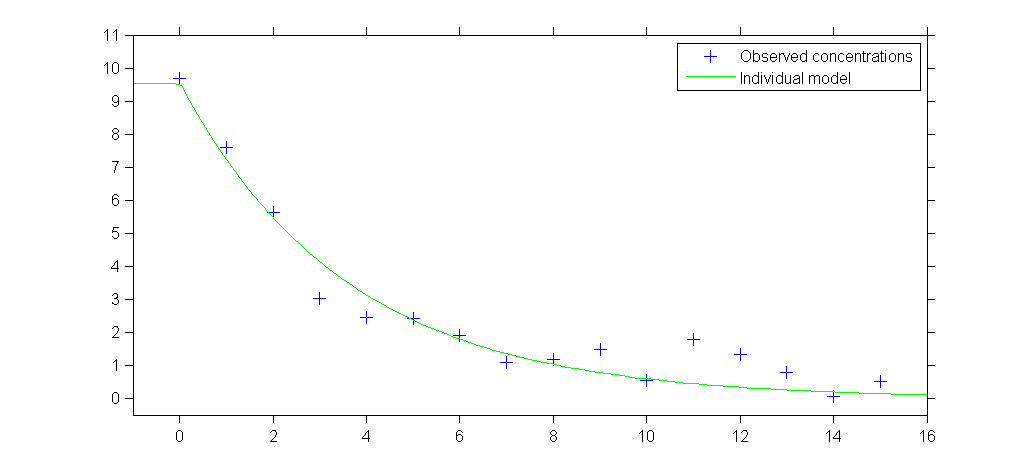
| + | |text=This second example involves weight data of rats, measured over 14 weeks in a setting of a sub-chronic toxicity study linked to Genetically Modified corn. | ||
| + | |image = intro2.png}} | ||
| + | |||
| + | |||
| + | {{ExampleWithImage | ||
| + | |text= Here, the data are fluorescence intensities measured over time during a cellular biology experiment. | ||
| + | |image=intro3.png }} | ||
| − | |||
| − | |||
| + | {{ExampleWithImage | ||
| + | |text= Repeated measurements are not necessarily functions of time. For example, we may be interested in corn production as a function of fertilizer quantity. | ||
| + | |image= intro4.png}} | ||
| + | Bien que ces différents examples concernent des domaines très différents, les données sont toutes des données répétées recueillies sur plusieurs individus. Une approche de population est alors pertinente pour décrire et modéliser ces données: in population approaches, the study is not based on a single individual, but on several individuals from the same population. The modeling goal is thus twofold : to characterize the biological or physical phenomena observed for each individual and the variability seen between individuals. | ||
| + | Dans notre exemple sur les rats, le modèle doit intégrer un modèle de croissance, qui décrit comment le poids d'un rat augmente avec le temps ainsi qu'un modèle statistique qui décrit pourquoi ces cinétiques peuvent varier d'un rat à l'autre. L'objectif est donc d'obtenir une courbe "typique" de population (in red), et d'expliquer la variabilité des courbes individuelles (in green) autour de cette courbe de population. | ||
| + | ::[[File:intro5.png]] | ||
| − | + | Le modèle permettra d'expliquer une partie de cette variabilité par des covariables individuelles comme le sexe ou le régime (les rats 1 et 3 sont des mâles alors que les rats 2 et 4 sont des femelles), mais une partie restera non expliquée et sera considérée comme aléatoire. Intégrer dans un même modèle des effets considérés comme fixes et des effets considérés comme aléatoires conduit naturellement à l'utilisation de modèles à effets mixtes. | |
| − | + | Une approche alternative, mais équivalente, considère ce modèle comme un modèle hierarchique: chaque cinétique est décrite par un modèle individuel, et la variabilité entre les modèles individuels est décrite par un modèle de population. Dans le cas de modèles paramétriques, cela signifie que les observations d'un individu donné sont décrite par un modèle d'observations qui dépend d'un vecteur de paramètres individuels: c'est l'approche individuelle classique. L'approche de population est alors une extension directe de l'approche individuelle: on rajoute dans le modèle une composante qui décrit la variabilité de ces paramètres individuels au sein de la population. | |
| − | |||
| − | + | Un modèle est alors une distribution de probabilité jointe, qui peut facilement s'étendre au cas où d'autres variables du modèles sont considérées comme des variables aléatoires: covariates, population parameters, design, ... | |
| − | + | La structure hierarchique du modèle permet une décomposition naturelle de cette distribution jointe en un produit de distributions conditionnelles et marginales. | |
| − | |||
| − | + | Les modèles pour les paramètres individuels et les modèles pour les observations sont décrits dans le Chapitre "Models". En particulier, des modèles pour des observations continues, catégorielles, de comptage et de survie sont présentés et illustrés par différents exemples. Extensions for mixture models, hidden Markov Models ans Stochastic Differential Equation based models are also presented. | |
| + | Le Chapitre "Tasks & Tools" présente des exemples pratiques d'utilisation de ces modèles: [[Visualization|exploration et visualization]], [[Estimation]], [[Model evaluation#Model diagnostics | Model diagnostics ]], [[Model evaluation#Model selection| Model selection]], [[Simulation]]. Toutes les approches et méthodes proposées sont rigoureusement justifiées dans le Chapitre "Methods". | ||
| − | |||
| + | L'objectif principal d'un modèle est d'être utilisé. La modèlisation mathématique et la statistique restent des outils au service d'autres disciplines (biology, agronomy, environment, pharmacology, ldots), mais il est important que ces outils soient correctement utilisés. | ||
| + | Les différents logiciels utilisés dans ce wiki ont été développés dans cet esprit: ils sont au service du modélisateur, tout en respectant rigoureusement un formalisme mathématique cohérent et en utilisant des méthodes reconnues et justifiées théoriquement | ||
| + | Une distinction | ||
| + | |||
| + | |||
| + | Pourquoi $monolix$ & \mlxtran$ | ||
| − | |||
| + | <ul> | ||
| + | * An algorithm which allows us to maximize $\int \pypsi(\by,\bpsi ;\theta) \, d \bpsi$ with respect to $\theta$. | ||
| + | Each software package has its own algorithms implemented. It is not our goal here to rate and compare the various algorithms and implementations. We will use exclusively the SAEM algorithm as described in [[The SAEM algorithm for estimating population parameters]] and implemented in $\monolix$ as we are convinced by its theoretical properties and satisfied by its practical qualities: | ||
| − | + | ** The algorithms implemented in $\monolix$ including SAEM and its extensions (mixture models, hidden Markov models, SDE-based model, censored data, etc.) have been published in statistical journals. Furthermore, convergence of SAEM has been rigorously proved. | |
| + | ** The SAEM implementation in \monolix is extremely efficient for a wide variety of complex models. | ||
| − | * | + | ** The SAEM implementation in \monolix was done by the same group that proposed the algorithm and studied in detail its theoretical and practical properties. |
| + | </ul> | ||
| − | |||
| − | |||
| − | + | {{Next | |
| − | + | |link=The individual approach }} | |
Revision as of 14:27, 3 June 2013
La modélisation d'un phénomène biologique ou physique est généralement motivée par l'observation de ce phénomène, c'est à dire lorsque des données générées par ce phénomène peuvent être recueillies. Quoi de plus naturel par conséquent, que de commencer par regarder quelques données ?
This first graphics display the viral load of four patients with hepatitis C who start a treatment at time $t=0$.
|
File:Intro1.png |
This second example involves weight data of rats, measured over 14 weeks in a setting of a sub-chronic toxicity study linked to Genetically Modified corn.
|
|
Here, the data are fluorescence intensities measured over time during a cellular biology experiment.
|
File:Intro3.png |
Repeated measurements are not necessarily functions of time. For example, we may be interested in corn production as a function of fertilizer quantity.
|
File:Intro4.png |
Bien que ces différents examples concernent des domaines très différents, les données sont toutes des données répétées recueillies sur plusieurs individus. Une approche de population est alors pertinente pour décrire et modéliser ces données: in population approaches, the study is not based on a single individual, but on several individuals from the same population. The modeling goal is thus twofold : to characterize the biological or physical phenomena observed for each individual and the variability seen between individuals.
Dans notre exemple sur les rats, le modèle doit intégrer un modèle de croissance, qui décrit comment le poids d'un rat augmente avec le temps ainsi qu'un modèle statistique qui décrit pourquoi ces cinétiques peuvent varier d'un rat à l'autre. L'objectif est donc d'obtenir une courbe "typique" de population (in red), et d'expliquer la variabilité des courbes individuelles (in green) autour de cette courbe de population.
Le modèle permettra d'expliquer une partie de cette variabilité par des covariables individuelles comme le sexe ou le régime (les rats 1 et 3 sont des mâles alors que les rats 2 et 4 sont des femelles), mais une partie restera non expliquée et sera considérée comme aléatoire. Intégrer dans un même modèle des effets considérés comme fixes et des effets considérés comme aléatoires conduit naturellement à l'utilisation de modèles à effets mixtes.
Une approche alternative, mais équivalente, considère ce modèle comme un modèle hierarchique: chaque cinétique est décrite par un modèle individuel, et la variabilité entre les modèles individuels est décrite par un modèle de population. Dans le cas de modèles paramétriques, cela signifie que les observations d'un individu donné sont décrite par un modèle d'observations qui dépend d'un vecteur de paramètres individuels: c'est l'approche individuelle classique. L'approche de population est alors une extension directe de l'approche individuelle: on rajoute dans le modèle une composante qui décrit la variabilité de ces paramètres individuels au sein de la population.
Un modèle est alors une distribution de probabilité jointe, qui peut facilement s'étendre au cas où d'autres variables du modèles sont considérées comme des variables aléatoires: covariates, population parameters, design, ... La structure hierarchique du modèle permet une décomposition naturelle de cette distribution jointe en un produit de distributions conditionnelles et marginales.
Les modèles pour les paramètres individuels et les modèles pour les observations sont décrits dans le Chapitre "Models". En particulier, des modèles pour des observations continues, catégorielles, de comptage et de survie sont présentés et illustrés par différents exemples. Extensions for mixture models, hidden Markov Models ans Stochastic Differential Equation based models are also presented.
Le Chapitre "Tasks & Tools" présente des exemples pratiques d'utilisation de ces modèles: exploration et visualization, Estimation, Model diagnostics , Model selection, Simulation. Toutes les approches et méthodes proposées sont rigoureusement justifiées dans le Chapitre "Methods".
L'objectif principal d'un modèle est d'être utilisé. La modèlisation mathématique et la statistique restent des outils au service d'autres disciplines (biology, agronomy, environment, pharmacology, ldots), mais il est important que ces outils soient correctement utilisés.
Les différents logiciels utilisés dans ce wiki ont été développés dans cet esprit: ils sont au service du modélisateur, tout en respectant rigoureusement un formalisme mathématique cohérent et en utilisant des méthodes reconnues et justifiées théoriquement
Une distinction
Pourquoi $monolix$ & \mlxtran$
<ul>
* An algorithm which allows us to maximize $\int \pypsi(\by,\bpsi ;\theta) \, d \bpsi$ with respect to $\theta$.
Each software package has its own algorithms implemented. It is not our goal here to rate and compare the various algorithms and implementations. We will use exclusively the SAEM algorithm as described in [[The SAEM algorithm for estimating population parameters]] and implemented in $\monolix$ as we are convinced by its theoretical properties and satisfied by its practical qualities:
** The algorithms implemented in $\monolix$ including SAEM and its extensions (mixture models, hidden Markov models, SDE-based model, censored data, etc.) have been published in statistical journals. Furthermore, convergence of SAEM has been rigorously proved.
- The SAEM implementation in \monolix is extremely efficient for a wide variety of complex models.
- The SAEM implementation in \monolix was done by the same group that proposed the algorithm and studied in detail its theoretical and practical properties.
