Difference between revisions of "The individual approach"
m |
m |
||
| Line 15: | Line 15: | ||
* $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters | * $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters | ||
* $(t_1,t_2,\ldots , t_n)$ : observation times | * $(t_1,t_2,\ldots , t_n)$ : observation times | ||
| − | * $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\ | + | * $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\Epsilon({\varepsilon_j}) =0$) |
* $g$ : { residual error model} | * $g$ : { residual error model} | ||
* $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors ($Var({\bar{\varepsilon_j}}) =1$) | * $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors ($Var({\bar{\varepsilon_j}}) =1$) | ||
| Line 36: | Line 36: | ||
where | where | ||
\begin{equation} | \begin{equation} | ||
| − | L(\psi ; y_1,y_2,\ldots,y_j) \ | + | L(\psi ; y_1,y_2,\ldots,y_j) \eq{def} p_Y( y_1,y_2,\ldots,y_j ; \psi) |
\end{equation} | \end{equation} | ||
Revision as of 17:21, 28 January 2013
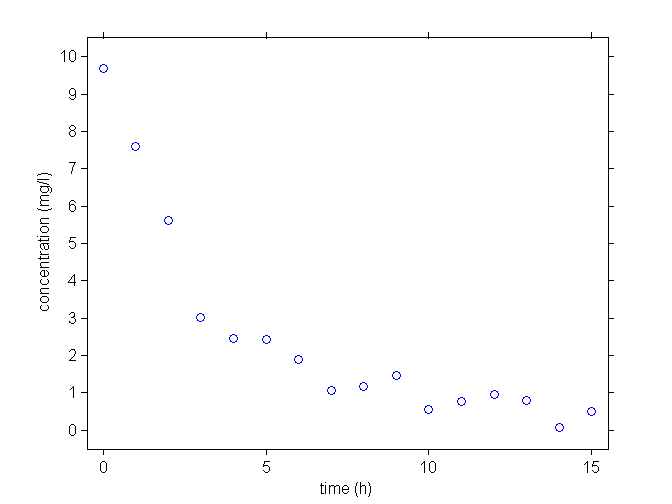
An example of continuous data from a single individual
A model for continuous data:
\begin{eqnarray*}
y_{j} &=& f(t_j ; \psi) + \varepsilon_j \quad ; \quad 1\leq j \leq n \\
&=& f(t_j ; \psi) + g(t_j ; \psi) \bar{\varepsilon_j}
\end{eqnarray*}
- $f$ : { structural model}
- $\psi=(\psi_1, \psi_2, \ldots, \psi_d)$ : vector of parameters
- $(t_1,t_2,\ldots , t_n)$ : observation times
- $(\varepsilon_j, \varepsilon_2, \ldots, \varepsilon_n)$ : residual errors ($\Epsilon({\varepsilon_j}) =0$)
- $g$ : { residual error model}
- $(\bar{\varepsilon_1}, \bar{\varepsilon_2}, \ldots, \bar{\varepsilon_n})$ : normalized residual errors ($Var({\bar{\varepsilon_j}}) =1$)
Some tasks in the context of modelling, {\i.e.} when a vector of observations $(y_j)$ is available:
- Simulate a vector of observations $(y_j)$ for a given model and a given parameter $\psi$,
- Estimate the vector of parameters $\psi$ for a given model,
- Select the structural model $f$
- Select the residual error model $g$
- Assess/validate the selected model
Maximum likelihood estimation of the parameters:
\begin{equation}
'"`UNIQ-MathJax18-QINU`"' maximizes '"`UNIQ-MathJax19-QINU`"' \bar{\varepsilon_i} \sim_{i.i.d} {\cal N}(0,1)'"`UNIQ-MathJax20-QINU`"'y_i'"`UNIQ-MathJax21-QINU`"'(y_1, y_2, \ldots y_n)'"`UNIQ-MathJax22-QINU`"'\times'"`UNIQ-MathJax23-QINU`"'y_{j} = f(t_j ; \phi) + a \, \teps_j'"`UNIQ-MathJax24-QINU`"'g=a+b*f'"`UNIQ-MathJax25-QINU`"'g=a'"`UNIQ-MathJax26-QINU`"'g=b\, f'"`UNIQ-MathJax27-QINU`"'g=a+b f'"`UNIQ-MathJax28-QINU`"'u(y_j)'"`UNIQ-MathJax29-QINU`"'y_j'"`UNIQ-MathJax30-QINU`"'g=a+b*f'"`UNIQ-MathJax31-QINU`"'\log(y)=\log(f) + a\, \teps$
\end{tabbing}